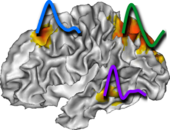
pyhrf.stats.random module

class pyhrf.stats.random.BetaGenerator(mean=0.5, var=0.1)

Bases: pyhrf.stats.random.RandomGenerator

Class encapsulating the beta random generator of numpy

generate(size)
class pyhrf.stats.random.GammaGenerator(mean=1.0, var=1.0)

Bases: pyhrf.stats.random.RandomGenerator

Class encapsulating the gamma random generator of numpy

generate(size)
class pyhrf.stats.random.GaussianGenerator(mean=0.0, var=1.0)

Bases: pyhrf.stats.random.RandomGenerator

Class encapsulating the gaussian random generator of numpy

generate(size)
class pyhrf.stats.random.IndependentMixtureLaw(states, generators)

Class handling the generation of values following an indenpendent mixture law. Requires the prior generator of label values.

generate()

Generate realisations of the mixture law.

class pyhrf.stats.random.LogNormalGenerator(meanLogN=1.0, varLogN=1.0)

Bases: pyhrf.stats.random.RandomGenerator

Class encapsulating the log normal generator of numpy

generate(size)
class pyhrf.stats.random.RandomGenerator

B Abstract class to ensure the definition of the function generate.

generate(size)
class pyhrf.stats.random.UniformGenerator(minV=0.0, maxV=1.0)

Bases: pyhrf.stats.random.RandomGenerator

Class encapsulating the random generator

generate(size)
class pyhrf.stats.random.ZeroGenerator

Bases: pyhrf.stats.random.RandomGenerator

Class encapsulating the null distribution !!!!!!!!!

generate(size)
pyhrf.stats.random.gm_sample(means, variances, props, n=1)
pyhrf.stats.random.rand(d0, d1, ..., dn)

Random values in a given shape.

Create an array of the given shape and populate it with random samples from a uniform distribution over [0, 1).

Parameters:d1, ..., dn (d0,) – The dimensions of the returned array, should all be positive. If no argument is given a single Python float is returned.
Returns:out – Random values.
Return type:ndarray, shape (d0, d1, ..., dn)

See also

random()

Notes

This is a convenience function. If you want an interface that takes a shape-tuple as the first argument, refer to np.random.random_sample .

Examples

>>> np.random.rand(3,2)
array([[ 0.14022471,  0.96360618],  #random
       [ 0.37601032,  0.25528411],  #random
       [ 0.49313049,  0.94909878]]) #random
pyhrf.stats.random.randn(d0, d1, ..., dn)

Return a sample (or samples) from the “standard normal” distribution.

If positive, int_like or int-convertible arguments are provided, randn generates an array of shape (d0, d1, ..., dn), filled with random floats sampled from a univariate “normal” (Gaussian) distribution of mean 0 and variance 1 (if any of the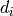 d_i are floats, they are first converted to integers by truncation). A single float randomly sampled from the distribution is returned if no argument is provided.

This is a convenience function. If you want an interface that takes a tuple as the first argument, use numpy.random.standard_normal instead.

Parameters:d1, ..., dn (d0,) – The dimensions of the returned array, should be all positive. If no argument is given a single Python float is returned.
Returns:Z – A (d0, d1, ..., dn)-shaped array of floating-point samples from the standard normal distribution, or a single such float if no parameters were supplied.
Return type:ndarray or float

See also

random.standard_normal()
Similar, but takes a tuple as its argument.

Notes

For random samples from 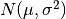N(\mu, \sigma^2), use:

sigma * np.random.randn(...) + mu

Examples

>>> np.random.randn()
2.1923875335537315 #random

Two-by-four array of samples from N(3, 6.25):

>>> 2.5 * np.random.randn(2, 4) + 3
array([[-4.49401501,  4.00950034, -1.81814867,  7.29718677],  #random
       [ 0.39924804,  4.68456316,  4.99394529,  4.84057254]]) #random
pyhrf.stats.random.rpnorm(n, m, s)

Random numbers from the positive normal distribution. rpnorm(n,m,s) is a vector of length n with random entries, generated from a positive normal distribution with mean m and standard deviation s.

Original matlab code from: (c) Vincent Mazet, 06/2005 Centre de Recherche en Automatique de Nancy, France vincent.mazet@cran.uhp-nancy.fr

Reference: V. Mazet, D. Brie, J. Idier, ‘Simulation of Positive Normal Variables using several Proposal Distributions’, IEEE Workshop Statistical Signal Processing 2005, july 17-20 2005, Bordeaux, France.

Adapted by Thomas VINCENT: thomas.vincent@cea.fr

pyhrf.stats.random.truncRandn(size, mu=0.0, sigma=1.0, a=0.0, b=inf)