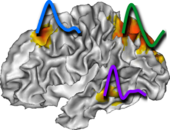
pyhrf.jde.nrl.bigaussian_drift module

class pyhrf.jde.nrl.bigaussian_drift.BiGaussMixtureParams_Multi_Sess_NRLsBar_Sampler(parameters=None, xmlHandler=None, xmlLabel=None, xmlComment=None)

Bases: pyhrf.jde.samplerbase.GibbsSamplerVariable

#TODO : comment

I_MEAN_CA = 0
I_VAR_CA = 1
I_VAR_CI = 2
L_CA = 1
L_CI = 0
NB_PARAMS = 3
PARAMS_NAMES = ['Mean_Activ', 'Var_Activ', 'Var_Inactiv']
P_ACTIV_THRESH = 'mean_activation_threshold'
P_HYPER_PRIOR = 'hyperPriorType'
P_MEAN_CA_PR_MEAN = 'meanCAPrMean'
P_MEAN_CA_PR_VAR = 'meanCAPrVar'
P_SAMPLE_FLAG = 'sampleFlag'
P_USE_TRUE_VALUE = 'useTrueValue'
P_VAL_INI = 'initialValue'
P_VAR_CA_PR_ALPHA = 'varCAPrAlpha'
P_VAR_CA_PR_BETA = 'varCAPrBeta'
P_VAR_CI_PR_ALPHA = 'varCIPrAlpha'
P_VAR_CI_PR_BETA = 'varCIPrBeta'
checkAndSetInitValue(variables)
computeWithJeffreyPriors(j, cardCIj, cardCAj)
computeWithProperPriors(j, cardCIj, cardCAj)
defaultParameters = {'initialValue': None, 'mean_activation_threshold': 4.0, 'varCAPrBeta': 0.5, 'varCIPrAlpha': 2.04, 'meanCAPrVar': 20.0, 'hyperPriorType': 'Jeffrey', 'varCIPrBeta': 2.08, 'sampleFlag': True, 'varCAPrAlpha': 2.01, 'useTrueValue': False, 'meanCAPrMean': 5.0}
finalizeSampling()
getCurrentMeans()
getCurrentVars()
getOutputs()
get_string_value(v)
linkToData(dataInput)
parametersComments = {'hyperPriorType': "Either 'proper' or 'Jeffrey'", 'mean_activation_threshold': 'Threshold for the max activ mean above which the region is considered activating'}
parametersToShow = ['initialValue', 'sampleFlag', 'mean_activation_threshold', 'useTrueValue', 'hyperPriorType', 'meanCAPrMean', 'meanCAPrVar', 'varCIPrAlpha', 'varCIPrBeta', 'varCAPrAlpha', 'varCAPrBeta']
sampleNextInternal(variables)
updateObsersables()
class pyhrf.jde.nrl.bigaussian_drift.NRL_Drift_Sampler(do_sampling=True, val_ini=None, contrasts={}, do_label_sampling=True, use_true_nrls=False, use_true_labels=False, labels_ini=None, ppm_proba_threshold=0.05, ppm_value_threshold=0, ppm_value_multi_threshold=array([ 0., 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1., 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2., 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3., 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. ]), mean_activation_threshold=4, rescale_results=False, wip_variance_computation=False)

Bases: pyhrf.jde.nrl.bigaussian.NRLSampler

Class handling the Gibbs sampling of Neural Response Levels in the case of joint drift sampling.

computeVarYTildeOpt(varXh)
sampleNextInternal(variables)
sampleNrlsSerial(rb, h, varCI, varCA, meanCA, gTg, variables)
class pyhrf.jde.nrl.bigaussian_drift.NRL_Drift_SamplerWithRelVar(do_sampling=True, val_ini=None, contrasts={}, do_label_sampling=True, use_true_nrls=False, use_true_labels=False, labels_ini=None, ppm_proba_threshold=0.05, ppm_value_threshold=0, ppm_value_multi_threshold=array([ 0., 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1., 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2., 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3., 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. ]), mean_activation_threshold=4, rescale_results=False, wip_variance_computation=False)

Bases: pyhrf.jde.nrl.bigaussian.NRLSamplerWithRelVar

Class handling the Gibbs sampling of Neural Response Levels in the case of joint drift sampling and relevant variable.

computeVarYTildeOptWithRelVar(varXh, w)
sampleNextInternal(variables)
sampleNrlsSerialWithRelVar(rb, h, gTg, variables, w, t1, t2)
class pyhrf.jde.nrl.bigaussian_drift.NRLsBar_Drift_Multi_Sess_Sampler(do_sampling=True, val_ini=None, contrasts={}, do_label_sampling=True, use_true_nrls=False, use_true_labels=False, labels_ini=None, ppm_proba_threshold=0.05, ppm_value_threshold=0, ppm_value_multi_threshold=array([ 0., 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1., 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2., 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3., 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. ]), mean_activation_threshold=4, rescale_results=False, wip_variance_computation=False)

Bases: pyhrf.jde.nrl.bigaussian.NRLSampler

Class handling the Gibbs sampling of Neural Response Levels in the case of joint drift sampling.

checkAndSetInitValue(variables)
linkToData(dataInput)
sampleNextAlt(variables)
sampleNextInternal(variables)
sampleNrlsSerial(varCI, varCA, meanCA, variables)
samplingWarmUp(variables)

#TODO : comment

pyhrf.jde.nrl.bigaussian_drift.permutation(x)

Randomly permute a sequence, or return a permuted range.

If x is a multi-dimensional array, it is only shuffled along its first index.

Parameters:x (int or array_like) – If x is an integer, randomly permute np.arange(x). If x is an array, make a copy and shuffle the elements randomly.
Returns:out – Permuted sequence or array range.
Return type:ndarray

Examples

>>> np.random.permutation(10)
array([1, 7, 4, 3, 0, 9, 2, 5, 8, 6])

>>> np.random.permutation([1, 4, 9, 12, 15])
array([15,  1,  9,  4, 12])

>>> arr = np.arange(9).reshape((3, 3))
>>> np.random.permutation(arr)
array([[6, 7, 8],
       [0, 1, 2],
       [3, 4, 5]])
pyhrf.jde.nrl.bigaussian_drift.rand(d0, d1, ..., dn)

Random values in a given shape.

Create an array of the given shape and populate it with random samples from a uniform distribution over [0, 1).

Parameters:d1, ..., dn (d0,) – The dimensions of the returned array, should all be positive. If no argument is given a single Python float is returned.
Returns:out – Random values.
Return type:ndarray, shape (d0, d1, ..., dn)

See also

random()

Notes

This is a convenience function. If you want an interface that takes a shape-tuple as the first argument, refer to np.random.random_sample .

Examples

>>> np.random.rand(3,2)
array([[ 0.14022471,  0.96360618],  #random
       [ 0.37601032,  0.25528411],  #random
       [ 0.49313049,  0.94909878]]) #random
pyhrf.jde.nrl.bigaussian_drift.randn(d0, d1, ..., dn)

Return a sample (or samples) from the “standard normal” distribution.

If positive, int_like or int-convertible arguments are provided, randn generates an array of shape (d0, d1, ..., dn), filled with random floats sampled from a univariate “normal” (Gaussian) distribution of mean 0 and variance 1 (if any of the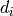 d_i are floats, they are first converted to integers by truncation). A single float randomly sampled from the distribution is returned if no argument is provided.

This is a convenience function. If you want an interface that takes a tuple as the first argument, use numpy.random.standard_normal instead.

Parameters:d1, ..., dn (d0,) – The dimensions of the returned array, should be all positive. If no argument is given a single Python float is returned.
Returns:Z – A (d0, d1, ..., dn)-shaped array of floating-point samples from the standard normal distribution, or a single such float if no parameters were supplied.
Return type:ndarray or float

See also

random.standard_normal()
Similar, but takes a tuple as its argument.

Notes

For random samples from 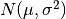N(\mu, \sigma^2), use:

sigma * np.random.randn(...) + mu

Examples

>>> np.random.randn()
2.1923875335537315 #random

Two-by-four array of samples from N(3, 6.25):

>>> 2.5 * np.random.randn(2, 4) + 3
array([[-4.49401501,  4.00950034, -1.81814867,  7.29718677],  #random
       [ 0.39924804,  4.68456316,  4.99394529,  4.84057254]]) #random